진료수행평가에서 가교-스테이션을 이용한 점수 동등화
Abstract
Purpose:
This study examined the use of the Tucker linear equating method in producing an individual student’s score in 3 groups with bridging stations over 3 consecutive days of the clinical performance examination (CPX) and compared the differences in scoring patterns by bridging number.
Methods:
Data were drawn from 88 examinees from 3 different CPX groups―DAY1, DAY2, and DAY3―each of which comprised of 6 stations. Each group had 3 common stations, and each group had 2 or 3 stations that differed from other groups. DAY1 and DAY3 were equated to DAY2. Equated mean scores and standard deviations were compared with the originals. DAY1 and DAY3 were equated again, and the differences in scores (equated score-raw score) were compared between the 3 sets of equated scores.
Results:
By equating to DAY2, DAY1 decreased in mean score from 58.188 to 56.549 and in standard deviation from 4.991 to 5.046, and DAY3 fell in mean score from 58.351 to 58.057 and in standard deviation from 5.546 to 5.856, which demonstrates that the scores of examinees in DAY1 and DAY2 were accentuated after use of the equation. The patterns in score differences between the equated sets to DAY1, DAY2, and DAY3 yielded information on the soundness of the equating results from individual and overall comparisons.
Conclusion:
To generate equated scores between 3 groups on 3 consecutive days of the CPX, we applied the Tucker linear equating method. We also present a method of equating reciprocal days to the anchoring day as much as bridging stations.
Keywords: Equation, Educational measurement, Clinical competence
서론
임상수행능력을 평가하는 객관구조화진료시험(objective structured clinical examination, OSCE) 혹은 임상수행시험(clinical performance examination, CPX)은 실제 진료 현장과 유사한 환경에서 이루어지는 환자 진료 형태, 즉 의사-환자 간 면담과 신체진찰로부터 수집하는 정보, 임상 추론 및 결정, 환자교육 및 관리 등을 표준화하여 시험 형태로 만들어 현재 대부분의 의과대학들은 임상 실습 교육 후 학생들의임상 수행 능력을 평가하고 있다[ 1, 2]. 아울러 진료수행평가에서 학생들의 수행 정도를 타당하고 공정하게 평가하는 것이 중요한 문제인데 표준화 환자를 이용한 진료수행평가는 그 특성상 여러 날에 걸쳐 시험이 시행되는 경우가 많다. 즉, station당 10분 이상의 시간이 소요되고 여러 개의 증례를 사용해야 하므로 학생 수가 많은 대학의 경우 이를 하루에 시행하는 것은 현실적으로 매우 어렵다. 또한 매일 동일한 시험 문항으로 시험을 치른다면 정보 공유 가능성 때문에 평가의 신뢰성에 대한 우려가 존재할 것이다. 동일하지 않은 시험 문항조합과 조건으로부터 모든 피험자의 시험 점수가 산출되어야 하는 경우에 학생들의 원점수는 동등화(equation) 과정을 거친 전환 점수로서 제시되어야 한다. 이처럼 동등화가 필요한 경우에 각 문항 조합에 어느 정도의 문항을 공통적으로 포함시키고 이를 통계적으로 처리하여 동등화 점수를 얻을 수 있는데 이러한 공통문항을 ‘가교문항(anchor item)’이라고 한다. 본 연구에서는 시험 시행일에 따라 CPX의 문항 조합을 달리하여, 총 10개의 문항 중 매일 6개의 문항 조합으로 3일간 시험을 실시하였는데 이 중 3개는 공통문항이었고 다시 조합 간 0~1개의 추가 공통문항을 배정하였다. 이를 통하여 학생들이 어떤 문항이 출제될지에 대한 관심을 떨어뜨리고 정상적인 시험 준비를 하도록 하는 효과는 있었으나, 조합별 문항이 다름에 따라 학생들의 성적을 공정하게 해석하고 반영하기 위하여 검사동등화 과정을 통해 시험 성적에 대한 통인처리를 할 필요성이 생겼다. 검사동등화를 실제 활용하는 대표적인 예는 Test of English for International Communication(TOEIC), American College Testing (ACT) 및 Scholastic Aptitude Test (SAT) 등이며 국내에서는 1985년 검사동등화의 개념이 국내에 소개된 이래로 주로 지필 시험 자료를 대상으로 동등화 방법 비교, 가교문항 관련 연구, 검사 특성, 학업 성취도 변화 등의 선행 연구가 있다[ 3, 4, 5, 6, 7, 8, 9]. 한편 CPX와 같은 수행평가에서의 동등화 작업은 채점자, 적은 문항 수 등의 요인으로 다중선다형지필시험에 비하여 실행에 어려움이 많은 것으로 알려져 있다[ 10]. 이에, 본 연구에서는 수행평가의 일종인 CPX에서 적용할 수 있는 동등화 방법을 제안하고 동등화 과정의 수행 결과 실제로 문항별 응시자들에게 부여되는 점수의 특성 및 원점수와 동등화점수 간의 차이 등을 분석함을 목적으로 하였다.
대상 및 방법
1. 연구 대상
E의학전문대학원 4학년 86명 학생을 대상으로 진료수행평가(CPX)를 시행하였으며, 총 3일의 시험기간 중 각 학생은 무작위로 배정된 날짜에 하루 시험을 치렀는데, 첫째 날(이하DAY1)과 둘째 날(이하 DAY2)은 각각 36명, 셋째 날(이하 DAY3)은 14명이었다. 날짜별 시험 문항은 각각 6개를 배정하였고, 이 중 3개는 3일간 동일하였으며 나머지는 다른 문항을 배정하였는데 DAY1과 DAY2에는 3개의 공통문항 외에한 문항을 공통문항으로 추가하였고 DAY2와 DAY3도 공통문항 외에 다른 한 문항을 공통문항으로 추가했다( Fig. 1). 각각의 문항에서 학생은 10분 동안 표준화 환자를 대상으로 진료를 하였으며, 문항개발, 표준화 환자 훈련 및 채점 등 진료 수행평가의 전 과정은 서울·경기 CPX 컨소시엄의 운영지침에 따라 진행되었다[ 11].
2. 연구 방법
동등화의 방법은 피험자 집단의 특성, 수, 각 피험자가 치르는 검사의 수, 가교검사의 사용 여부 등에 따라 다양한데, 본 연구에서는 연구 대상 집단 및 검사의 특성에 따라 검사의 동등화 점수 산출은 시험일마다 시험을 치른 집단의 능력의 차이가 크지 않다는 가정과 두 점수의 분포가 비슷하다면 피험자의 수가 적더라도 정확한 결과를 얻을 수 있는 비동등집단 가교검사 설계에 적용되는 전통적인 방법 중 하나인 Tucker의 선형동등화 방법을 선택하여 적용하였다. 이를 산출하기 위해 시험일 각각에 대한 전체 점수와 시험일 모두에 공통인 3개 문항전체의 평균, 표준편차 및 분포를 구하여 비교하였다.
두 검사를 치른 집단이 동일한 모집단으로부터 표집되었다고 가정할 수 없을 때, 즉, 검사 X를 치른 집단은 모집단 1에서 표집된 표본이고, 검사 Y를 치른 집단은 모집단 2에서 표집된 표본일 때 두 검사의 점수는 자체의 난이도 차이뿐만 아니라 피험자들의 능력에도 차이가 혼동된 상태가 된다.
이에, 두 검사의 동등 점수를 찾아내기 위해서는 피험자 능력의 차이를 고려한 능력, 일반적으로 공통검사(가교검사 V)의 이용이 필요하다. 비동등집단 가교검사 동등화에서는 본검사 X, Y와 측정의 내용뿐만 아니라 통계적인 특성 또한 가능한 한 동일하도록 제작된 가교검사의 차이는 곧 두 모집단의 능력의 차이를 의미한다고 가정하여, 가교검사의 문항들은 두 모집단의 차이를 교정하는 데 사용된다[ 3, 5, 10]. Tucker의 선형동등화 방법은 두 피험자 집단의 능력의 차이가 크지 않다고 판단했을 때, 다음과 같은 가정을 만족하여야 하며 유도 및 계산식은 아래와 같다[ 10]. a. 검사 X의 점수와 가교검사 V의 점수와의 관계와 검사 Y의 점수와 가교검사 V의 관계는 집단 1과 집단 2에서 동일한 선형 회귀식을 갖는다.
b. 가교검사 V의 어떤 점수 하에서 검사 X의 조건부분산은 집단 1과 집단 2에서 동일하며, 검사 Y의 조건부분산도 마찬가지이다. 비동등집단 가교검사에서는 아래와 같은 식을 통해 선형 전환할 수 있다.
이러한 가정 하에 본 연구에서는 가교문항으로서 3~4개 문항으로 이루어진 가교검사(V)를 구성하였다. Tucker 방법을 유도하는 식의 예를 들면 다음과 같다.
우선, DAY2의 원점수로 다른 시험일의 점수를 변환하고자 할 때, 아래와 같이 검사 X의 결합 모집단의 평균과 표준편차를 계산하였다.
이를 적용하여 회귀선의 기울기를 계산하면 아래와 같다.
위에 계산한 회귀식의 기울기를 이용하여 검사 Y의 결합 모집단의 평균과 표준편차를 계산하면 아래와 같다.
위에 계산한 결합 모집단의 모수 추정치들(μ^ s(X), σ^ s(X),μ^ s(Y), σ^ s(Y))을 대입하면, 검사 X의 점수를 검사 Y의 점수에 선형 동등화하는 다음 함수식이 완성된다.
1) DAY2의 원점수로 다른 시험일의 점수를 변환
DAY1과 DAY2, DAY2과 DAY3은 각각 4개의 공통문항으로 구성되었고 DAY1과 DAY3은 3개의 공통문항으로 구성되어 있으므로 가교검사 수가 많은 동등화 식을 찾기 위해 DAY2의 원점수로 DAY1과 DAY3의 점수를 동등화하여 전환 점수를 구했으며 계산식은 다음과 같다.
a. DAY2의 원점수로 DAY1의 점수를 동등화하는 변환식
b. DAY2의 원점수로 DAY3의 점수를 동등화하는 변환식
2) DAY1과 DAY3의 원점수로 다른 날의 점수를 각각 변환
DAY1과 DAY3은 3개의 공통문항으로 구성되어 있어서 가교검사의 수에 따른 비교를 위해 DAY1과 DAY3의 원점수로 각각 다른 날의 점수를 동등화하여 전환 점수를 구했으며 계산식은 다음과 같다.
a. DAY1의 원점수로 DAY2의 점수를 동등화하는 변환식
b. DAY1의 원점수로 DAY3의 점수를 동등화하는 변환식
c. DAY3의 원점수로 DAY1의 점수를 동등화하는 변환식
d. DAY3의 원점수로 DAY2의 점수를 동등화하는 변환식
3) 각각의 경우에 원점수와 변환점수의 차이를 산포도로 비교하였다.
결과
1. 시험일자별 원점수 총점 비교와 공통문항의 총점비교
날짜별 시험군의 총점 평균(표준편차)은 각각 58.188 (4.911), 58.765 (5.665), 58.351 (5.546)로 차이가 거의 없었다( Table 1). 한편, 시험일 모두에 배정된 세 문항의 총점 평균(표준편차)은 각각 58.207 (12.954), 57.464 (12.938), 56.683 (12.058)로서 공통문항 점수로 비교해 봤을 때는 DAY1군 성적이 가장 높고 DAY3군 성적이 가장 낮았다( Table 2).
2. DAY2의 원점수로 다른 시험일의 점수를 변환
각각 4개의 공통문항으로 구성된 DAY1과 DAY2, DAY2과 DAY3 조합의 특성을 활용하여, DAY2 원점수를 기준으로 4개의 공통문항을 가교점수로 하여 Tucker의 선형동등화식을 만들어 동등화 점수를 산출하는 점수 분포는 Table 3과 같다. 원점수와 변환점수의 평균(표준편차)의 변화는 DAY1군이 58.188(4.991)에서 56.549 (5.046)로 감소하였고 DAY3군은 58.351(5.546)에서 58.057 (5.856)로 약간 감소하였다( Table 4).
3. 가교문항 수의 차이에 따른 동등화 점수 비교
가교문항 수에 의한 효과를 비교하기 위하여 공통문항이 3개인 DAY1과 DAY3 조합의 특성을 활용하여 DAY1, DAY3의 원점수를 각각 기준으로 3개의 공통문항을 가교점수로 한 Tucker의 선형동등화식을 만들어 동등화 점수를 산출하였으며 각각 경우의 평균(표준편차)을 비교하였다. DAY1 원점수를 기준으로 한 경우에는 DAY 2 평균점수는 1.631 증가하였고 DAY3은 거의 변화가 없었다. 또한 DAY3 원점수를 기준으로 Tucker의 선형동등화식을 만들어 동등화 점수를 산출한 경우 DAY1, DAY2의 평균점수의 변화는 각각 0.123,0.354점 증가하였다( Table 5). 기준 군에 따른 변환 점수 분포의 비교를 위해 X축은 학생들의 점수, Y축은 원점수와 동등화하여 변환된 점수와의 차이 점수를 가지고 표시한 결과는 Fig. 2와 같다. DAY2와 각각 4개씩의 가교문항을 가진 DAY1과 DAY3의 동등화 후 원점수와의 차이점수의 분포도( Fig. 2A)는 서로 양의 관계와 기울기를 보이는 반면 다른 날짜의 시험군과 3개와 4개의 가교문항을 각각 가진 DAY1을 기준으로 한 분포도(( Fig. 2B)는 양과 음의 관계가 교차하는 양상을 보이고 있으며, 또 다른 DAY2를 기준으로 한 경우( Fig. 2C)는 음의 관계와 기울기를 보였다.
고찰
검사의 주목적이 피험자들을 선발하는 것일 때 결과를 공정하게 해석하는 것은 무엇보다 중요하다. 이때에는 특정 유형의 검사를 치른 사람이 다른 사람보다 더 유리하거나 불리한 상황이 발생하지 않도록 하는 통계적인 조작이 필요하다. 검사의 문항 내용, 신뢰도, 난이도 수준과 범위까지 엄격하게 동일한 동형검사가 제작될 수 있다면 별도의 통계적 조작이 필요 없겠지만 실질적으로 엄격한 의미의 동형검사 또는 평행검사를 제작한다는 것은 불가능하다. 따라서 기능을 재는 검사가 여러 가지 유형으로 제작되고 실시되었을 때, 각 검사유형의 점수 수준을 공통 척도로 변환시키는 동등화 과정이 필요하다[ 3]. 학생들의 학력 변화 추이를 조사하고자 할 때에도 검사 동등화가 요구되며, TOEIC 등과 같이 다수의 수험일 중 선택하여 시험을 치르는 경우에도 필요하다. 본 연구 대상에서의 동등화검사 설계로는 비동등집단 가교검사 방법을 선택하였는데 이는 일반적으로 동등화 할 두 검사의 실시 간격이 있고, 두 피험자 집단의 동질성을 가정할 수 없는 경우에 가장 현실적인 설계이기 때문이다. 이 설계에서 가교검사의 역할이 매우 큰데 동등화검사 X와 Y의 문항 모집단과 가교검사의 문항 모집단은 같아야 하며, 집단 간 능력의 차이가 지나치게 크다든지 가교검사 문항 수가 전체 문항 수의 20% 이하로서 내용 대표성을 확보하지 못할 때 동등화 오차가 커진다[ 7]. Tucker의 선형동등화 방법은 전통적인 비동등집단 가교 검사법이며 두 검사의 표준점수가 같으면 동등점수로 간주하고, 동등관계를 산출하기 위해서 가교검사 결과를 바탕으로 하나의 모집단을 인위적으로 만들어 분석에 활용하는 것으로서 두 검사 점수의 분포가 비슷하다면 피험자 수가 적더라도 정확한 동등화 결과를 얻을 수 있다[ 3]. 본 연구에서는 공통문항을 포함한 날짜별 시험군의 점수를 동등화하기 위하여 가능하면 많은 수의 가교 station을 포함하는 조합인 DAY2의 원점수를 기준으로 DAY1과 DAY3의 동등화점수를 계산하여 최종점수로 하였다. 단순 평균 비교에서는 DAY1군이 DAY2나 DAY3보다 전체 점수, 세 개의 공통문항 점수 등에서 높아서( Tables 1, 2) 집단별 능력이 더나은 것처럼 보이나 동등화한 결과 DAY1의 전체 평균점수는 원점수보다 낮아지면서 DAY2군의 평균점수보다도 낮아졌다( Table 4). 이는 공통문항 외에 다른 문항들의 점수가 추가로 반영될 때 세 군 간의 동등화 효과를 나타낸다고 할 수 있으며, 이 효과는 DAY1 과 DAY3을 기준으로 동등화한 결과에서도 유사하게 나타나 두 경우 모두 DAY1군의 전체 평균점수는 DAY2보다 낮게 계산되었다( Table 5). 한편, 시험일별 전체 평균점수 변동과 개별 학생들의 동등화 작업 후 점수 변화와 어떤 관계인지를 보여주는 Fig. 2로 어느 점수대에서 변환 점수 폭이 큰지를 알 수 있으며 이는 동등화 결과 점수를 실제 성적으로 활용할 지를 결정할 때나 다른 동등화 방법을 이용한 결과와 비교할 때 도움이 될 수 있다[ 6]. 또한, Fig.2A에서 DAY1의 점수 변환 폭보다 DAY3의 점수 변환 폭이큰 것과 Fig. 2C에서 DAY2보다 DAY3의 점수 폭이 큰 것은 DAY3의 학생 수가 DAY1과 DAY2보다 적기 때문으로 해석되며 이는 Fig. 2B에서 DAY1과 DAY2의 점수 변환 폭이 다른 경우에 비해 크게 나타난 이유일 수 있다. CPX 시험은 해당 교육 및 평가 전문가가 개별 및 팀-작업을 통해 개발하여 내용 타당도를 높이고 채점 일치도 훈련을 통하여 채점에 주관성을 낮추기 위한 노력을 하고 있으나 수행평가의 특성상 채점자 요인이 동등화를 시행하는 데 문제로 작용될 수 있기 때문에 이에 대해서는 추후 연구가 필요할 것이다. 또한 본 연구에서는 Tucker의 선형동등화 방법을 이용하였지만 다른 동등화 설계의 적용 가능성, 여러 날에 걸친 대규모 시험에서는 어떤 방식의 가교 동등화 작업을 할 수 있는지가 향후 연구 과제일 수 있다.
결론적으로 본 연구에서는 실제 3일에 걸쳐 시행되는 CPX 시험에서 가교문항을 이용하여 동등화 점수를 산정하였으며 가교문항의 수에 따른 동등화 점수의 분표를 구하여 비교하였으며, CPX 시험의 운영 특성상 학생 수와 문항 수에 따라 수일에 걸쳐 시험이 실행되어야 하는 경우에 Tucker의 선형동등화 방법을 적용해 보되 최종 동등화 산정 점수는 동등화 조합들의 점수 분포를 비교하여 결정하는 것이 좋을 것으로 사료된다.
Fig. 1.
Case-Stations with Anchoring by Examination Day
VACC: Vaccination; AA: Acute abdomen; BACK: Back pain; CHEST: Chest discomfort; ARRHY: Arrhythmia.
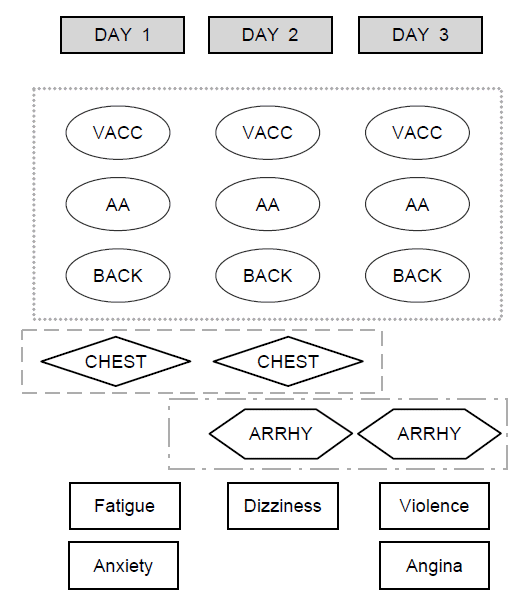
Fig. 2.
Comparisons of Score Differences (Equated Score–Raw Score) between 3 Tucker Methods by Equating to DAY2 (A), DAY3 (B), and DAY1 (C)

Table 1.
Descriptive Statistics from the Raw Scores of 3 Groups
|
Group |
No. |
Mean |
SD |
Skewness |
Kurtosis |
|
DAY1 |
36 |
58.188 |
4.991 |
0.431 |
-0.354 |
|
DAY2 |
36 |
58.765 |
5.665 |
0.444 |
0.637 |
|
DAY3 |
14 |
58.351 |
5.546 |
-0.593 |
-0.068 |
Table 2.
Comparison of Total Mean Scores of 3 Common Stations among 3 Groups
|
Group |
No. |
Mean |
SD |
Skewness |
Kurtosis |
|
DAY1 |
36 |
58.207 |
12.954 |
-0.290 |
0.461 |
|
DAY2 |
36 |
57.464 |
12.938 |
-0.569 |
0.461 |
|
DAY3 |
14 |
56.683 |
12.058 |
0.000 |
0.717 |
Table 3.
Equated Scores of DAY1 and DAY3 to DAY2 Raw Scores Using the Tucker Equating Method
|
Raw scores |
Equated scores to the DAY2 scores using Tucker equating method |
|
|
Day1 |
DAY3 |
|
0 |
-2.28 |
-3.56 |
|
2 |
-0.26 |
-1.45 |
|
4 |
1.76 |
0.66 |
|
6 |
3.79 |
2.77 |
|
8 |
5.81 |
4.89 |
|
10 |
7.83 |
7.00 |
|
12 |
9.85 |
9.11 |
|
14 |
11.87 |
11.22 |
|
16 |
13.90 |
13.33 |
|
18 |
15.92 |
15.45 |
|
20 |
17.94 |
17.56 |
|
22 |
19.96 |
19.67 |
|
24 |
21.98 |
21.78 |
|
26 |
24.01 |
23.89 |
|
28 |
26.03 |
26.01 |
|
30 |
28.05 |
28.12 |
|
32 |
30.07 |
30.23 |
|
34 |
32.10 |
32.34 |
|
36 |
34.12 |
34.45 |
|
38 |
36.14 |
36.57 |
|
40 |
38.16 |
38.68 |
|
42 |
40.18 |
40.79 |
|
44 |
42.21 |
42.9 |
|
46 |
44.23 |
45.01 |
|
48 |
46.25 |
47.13 |
|
50 |
48.27 |
49.24 |
|
52 |
50.29 |
51.35 |
|
54 |
52.32 |
53.46 |
|
56 |
54.34 |
55.57 |
|
58 |
56.36 |
57.69 |
|
60 |
58.38 |
59.80 |
|
62 |
60.40 |
61.91 |
|
64 |
62.43 |
64.02 |
|
66 |
64.45 |
66.13 |
|
68 |
66.47 |
68.25 |
|
70 |
68.49 |
70.36 |
|
72 |
70.51 |
72.47 |
|
74 |
72.54 |
74.58 |
|
76 |
74.56 |
76.69 |
|
78 |
76.58 |
78.81 |
|
80 |
78.60 |
80.92 |
|
82 |
80.62 |
83.03 |
|
84 |
82.65 |
85.14 |
|
86 |
84.67 |
87.25 |
|
88 |
86.69 |
89.37 |
|
90 |
88.71 |
91.48 |
|
92 |
90.73 |
93.59 |
|
94 |
92.76 |
95.70 |
|
96 |
94.78 |
97.81 |
|
98 |
96.80 |
99.93 |
|
100 |
98.82 |
102.04 |
Table 4.
Comparisons of Final Scores for Equating DAY1 and DAY3 to DAY2 Using the Tucker Equating Method
|
DAY 1 |
DAY2 |
DAY3 |
|
|
|
Raw |
Equated |
Raw |
Raw |
Equated |
|
Mean |
58.188 |
56.549 |
58.765 |
58.351 |
58.057 |
|
SD |
4.991 |
5.046 |
5.665 |
5.546 |
5.856 |
|
Skewness |
0.431 |
0.431 |
0.444 |
-0.593 |
-0.593 |
|
Krutosis |
-0.354 |
-0.354 |
0.637 |
-0.068 |
-0.068 |
Table 5.
Comparisons of Final Mean Scores Equated to Reciprocal DAY Using the Tucker Equating Method
|
Equating |
DAY1 |
DAY2 |
DAY3 |
|
To DAY2 |
56.549 |
58.765 |
58.057 |
|
To DAY3 |
58.311 |
59.019 |
58.351 |
|
To DAY1 |
58.188 |
60.396 |
58.252 |
REFERENCES
1. Harden RM, Gleeson FA. Assessment of clinical competence using an objective structured clinical examination (OSCE). Med Educ 1979;13:41-54.   2. Adamo G. Simulated and standardized patients in OSCEs: achievements and challenges 1992-2003. Med Teach 2003;25:262-270.   3. Nam HW. Geomsa dongdeunghwa bangbeop. Seoul, Korea: Kyoyookbook; 2001:45-50.
4. Kim HC. A comparison of equating methods for elective subjects scores of College Scholastic Ability Test by simulation (II): analysis of standard deviation of equated scores and average of equated scores for each common test score. Korean J Educ Res 2003;41:115-133.
5. Kim JC, Kim SH. The calibration of the mathematical scholastic ability changes of middle school students through vertical equating including anchor items. J Curric Eval 2006;9:275-298.
6. Boo JY. A comparison of scholastic performance in Korean Language, English, and Mathematics through vertical equating methods using empirical data between grades. J Educ Eval 2005;18:81-100.
7. Kim YJ, Lee GM, Kang SJ, Jeon SY. An investigation of the effect of anchor test length and non-equivalency of equating groups on equating. J Educ Eval 2009;22:1133-1160.
8. Chon KH, Seong TJ. A comparison of the item characteristics and examinee ability in the College Scholastic Ability Test (CSAT) foreign language section using equating. J Educ Eval 2003;16:87-104.
9. Boo JY. Issues in equating: equivalency, equating errors, equating pre-test and post-test. J Educ Eval 1999;12:43-64.
10. Kolenn MJ, Brennan RL. Test equating, scaling, and linking: methods and practices. 2nd ed. New York, USA: Springer; 2004:320-323.
11. Park HK. 3-year experience of Seoul·Gyeonggi CPX consortium. Paper presented at: CPX Symposium; 2006 December 12; Seoul, Korea?.
|
|














