
|


|

AbstractPurpose:The reliability of test is determined by each items' characteristics. Item analysis is achieved by classical test theory and item response theory. The purpose of the study was to compare the discrimination indices with item response theory using the Rasch model.
Methods:Thirty‐one 4th‐year medical school students participated in the clinical course written examination, which included 22 A‐type items and 3 R‐type items. Point biserial correlation coefficient (Cpbs) was compared to method of extreme group (D), biserial correlation coefficient (Cbs), item‐total correlation coefficient (Cit), and corrected item‐total correlation coeffcient (Ccit). Rasch model was applied to estimate item difficulty and examinee's ability and to calculate item fit statistics using joint maximum likelihood.
Results:Explanatory power (r2) of Cpbs is decreased in the following order: Ccit (1.00), Cit (0.99), Cbs (0.94), and D (0.45). The ranges of difficulty logit and standard error and ability logit and standard error were -0.82 to 0.80 and 0.37 to 0.76, -3.69 to 3.19 and 0.45 to 1.03, respectively. Item 9 and 23 have outfit ≥1.3. Student 1, 5, 7, 18, 26, 30, and 32 have fit ≥1.3.
서론한 가지 검사는 수십 개의 문항들로 구성되며 각 문항의 특성이 그 검사의 신뢰도를 결정한다. 고전검사이론과 문항반응이론으로 문항의 특성을 정량적으로 평가할 수 있다. 문항변별도는 수험자들의 능력을 변별하는 정도를 나타내는 지표다. 대표적인 변별도 지수(item discrimination index)는 양극집단법(method of extreme group, D)과 다양한 상관계수로 측정할 수 있고 여기에는 점양분상관계수(point biserial correlation coefficient, Cpbs), 양분상관계수(biserial correlation coefficient, Cbs), 문항-총점상관(item-total correlation coefficient, Cit) 및 교정된 문항-총점상관(corrected item-total correlation coefficient, Ccit)이 있다[1,2,3]. 변별도 지수마다 계산하는 방법이 다르기 때문에 각 지표의 특성을 확인하는 것은 중요하다.
고전검사이론에 의하면 수험자의 능력은 검사의 곤란도에 영향을 받기 때문에 수험자의 능력을 추정하는 것은 어렵다고 한다. 그러나, 문항반응이론에 따르면 수험자의 능력과 검사의 곤란도는 독립적이기 때문에 서로에게 영향을 주지 않는다고 하며 이것을 피험자 능력 불변성이라 한다[4]. 라쉬모형(Rasch model)은 문항의 곤란도(difficulty, δ)와 수험자의 능력(ability, θ)을 추정하는 1-모수모형이다[5]. 컴퓨터를 이용한 개별적응검사(computerized adaptive testing)와 같은 분야에서 라쉬모형을 이용하고 있고 문항의 곤란도와 수험자의 능력과 같은 모수(parameter)의 추정은 통계적인 방법을 사용한다.
의학전문대학원 4학년 과정의 임상시험 결과에서 변별도 지수들과 라쉬모형에 의한 문항반응이론을 비교하기 위해서 본 연구를 수행하였다.
대상 및 방법수험자는 의학전문대학원 4학년 학생들이며 34명이 시험에 참여하였다. 검사는 어떤 임상과목의 필기시험이며, 22개의 A형 문항들과 3개의 R형 문항이 총 25문항으로 구성되었다. 검사의 신뢰도(Cronbach's α)는 0.70, 측정의 표준오차(standard error of measurement, SEM)는 ±2.20점이었다[6].
1. 문항 변별도 지수들의 특성과 상관관계문항 변별도 지수들은 양극집단법 양분상관계수, 문항-총점상관계수, 교정된 문항-총점상관계수 그리고 점양분상관계수로 계산하였다. 표준적인 방법으로 알려진 점양분상관계수를 다른 방법의 지수들과 상관분석하였다.
2. 문항의 곤란도와 수험자의 능력을 추정하기 위한 라쉬모형의 적용n명의 피험자가 m개의 문항으로 구성된 검사를 시행할 때, 문항반응을 χij로 나타낼 수 있다. 라쉬모형에서 χij는 각 문항의 곤란도와 각 수험자의 능력에 의해 결정되므로 다음과 같이 정리할 수 있다.
여기서 문항 곤란도와 수험자 능력을 포함한 모수들은 결합최대우도법(joint maximum likelihood)을 사용하여 추정하고 이 과정은 다음과 같다[8].
1) 곤란도의 추정량(estimates)을 ∆와 능력의 추정량을 θ라고 할 때, 어떤 검사의 문항반응에서 정답능력비의 로그(ability logit)와 오답문항비의 로그(difficulty logit)는 다음과 같은 등식으로 나타낼 수 있다.
Equation 3에서 ∆i가 0에 수렴하도록 하기 위해서 그것의 평균값과 차를 구하고 그 결과를 ∆iʹ라고 한다.
2) χij의 기대값을 E라 하고 Equation 2에 적용할 때, 기대값은 다음과 같이 구할 수 있다.
이러한 추정을 하는 동안 분산(variance, V)은 다음과 같다.
3) 이때, 문항반응과 기댓값의 차이가 잔차(residual, R)가 되며 다음과 같이 정리할 수 있다.
4) 잔차가 가능한 적을 때까지 1), 2), 3)의 과정을 반복한다[9]. 반복 횟수가 s번째일 때, 이러한 과정은 다음과 같이 요약할 수 있으며, 본 연구에서 반복 횟수는 9회로 하였다.
Equation 7과 같이 문항반응과 Equation 10의 차이가 잔차다. 이때 능력과 곤란도 추정의 표준오차(standard error, SE)는 다음과 같이 구할
3. 라쉬모형의 적합도(Fit statistics for Rasch model)또한, 수험자와 문항의 infit 적합도(infit statistics, v)는 다음과 같다[12].
4. 통계 분석점양분상관계수와 다른 분별도 지표들 사이에 상관분석을 하고 회귀분석하여 회귀 방정식으로 나타냈다. 문항의 난이도와 수험자의 능력을 추정하기 위한 라쉬모형은 Excel 프로그램 version 12.0 (Microsoft Co., Redmond, USA)으로 작성하였다. 라쉬모형에 대한 문항반응의 적합도와 변별도 사이의 관계를 확인하였다. 수험자‐문항 분포도를 작성하여 검사가 수험자의 능력에 적절한 문항 곤란도를 갖는 문항들로 구성된 검사였는지 확인하였다. 추정된 문항들의 곤란도와 수험자들의 능력에 대한 평균과 표준편차를 구하고 ±2 표준편차 이상의 분포를 보이는 문항과 수험자를 확인하였다.
결과변별도 지표들 사이의 상관관계에서 점양분상관계수에 대한 설명력(r2)은 교정된 문항·총점상관계수, 문항·총점상관계수, 양분상관계수, 그리고 양극집단법의 순서로 감소하였다(Fig. 1). 교정된 문항·총점상관계수는 1이었고 양극집단법은 0.45로 낮았으며 Table 1에 각각의 회귀방정식을 정리하였다.
본 연구에서 종합최대우도 추정법을 사용하여 라쉬모형을 적용하였고[13], 9회 반복할 때 능력 추정에 대한 잔차제곱의 합(sum of squared residuals, SSR)이 3.59x10-8에 도달하였다. 라쉬모형에 의한 수험자 능력과 문항 곤란도의 추정과 표준오차를 Table 2와 3에 요약하였다. 수험자 능력과 표준편차의 범위는 -0.82~0.80과 0.37~0.76이고, 문항 곤란도와 표준편차의 범위는 -3.69~3.19와 0.45~1.03였다. 수험자의 백분율 점수와 능력 모수와 표준오차를 Fig. 2에 나타냈다. 능력 모수가 클수록 득점수가 증가하며 S자 모양을 형성한다. 라쉬모형에 대한 문항반응의 적합도는 Table 2와 3에 정리하였다. 1.3 이상을 부적합한 문항과 수험자로 판단할 때, 문항 9번과 23번, 그리고 학생 1번, 5번, 7번, 18번, 26번, 30번 및 32번이 여기에 속했다.
수험자-문항 분포도는 Fig. 3에 나타냈다. 문항 난이도가 수험자 능력에 비해 낮게 구성된 것을 알 수 있고 고능력자에게 알맞은 문항을 제공하지 못한 것을 보여준다. 수험자 능력 logit과 문항 난이도 logit의 평균과 표준편차는 각각 0.00±0.49와 0.71±0.87이었다. 따라서 표준편차의 2배 값을 벗어나는 문항은 없었고, 학생 4번과 32번은 평균에서 표준편차의 2배 범위 밖에 위치한다.
고찰본 연구에서 점양분상관계수에 대한 교정된 문항-총점 상관계수의 설명력이 1.00이기 때문에 점양분상관계수와 일치하였으나 기울기가 1.02로 약간 증가하였다. Ebel은 분별도 지수가 0.4 이상이면 높고 0.2 미만일 때 낮다고 하였다[14]. 이 변별도 지수는 문항과 피험자의 수 그리고 상위군과 하위군의 선정기준에 영향을 받는다. 점양분상관계수와 함께 교정된 문항총점상관계수와 문항총점상관계수가 우수한 변별력 지표들이지만 각각의 특성은 서로 다르다. 교정된 문항총점상관계수는 점양분상관계수보다 기울기가 증가하기 때문에 양극단에서 과장될 수 있다. 문항총점상관계수와 양분상관계수는 점양분상관계수보다 높게 측정되기 때문에 실제보다 과대평가될 수 있다.
표본수가 적은 설문지나 심리검사를 분석할 때, 라쉬모형은 신뢰할만한 결과를 보여 주며 준거지향 평가와 평가기준 설정에도 라쉬모형을 적용하고 있다[15]. 라쉬모형에서 문항 곤란도과 수험자 능력을 추정하는 방법들은 종합최대우도 추정법과 베이지안 추정법이다. 종합최대우도 추정법은 만점자나 영점자의 능력을 추정할 수 없고, 베이지안 추정법은 초기 추정값이 최종 추정값에 영향을 받는다고 한다[13,16,17,18].
어떤 모형에 의한 반응의 적합도(fit statistics)로 검사의 일차원성(unidimensionality)을 확인할 수 있기 때문에 검사의 내용 타당도(content validity)의 중요한 지표가 될 수 있다[19]. 라쉬모형을 적용할 때 관찰된 문항반응의 적합도는 infit과 outfit 적합도로 문항과 수험자 모두를 평가할 수 있다[20]. Infit 적합도는 예측 가능한 관찰들에 민감한 반면 outfit 적합도는 동떨어진 관찰들에 민감하다고 한다. 적합도는 0에서 무한의 값을 가질 수 있고 적합도 1은 측정시스템의 왜곡이 없다는 것을 의미한다. 적합도가 1 미만이면 너무 예상이 가능한 반응을 보이는 것이고, 1보다 크면 기대로부터 벗어난 반응을 의미한다. 적합도가 0.7~1.3 사이의 값을 보일 때 우수한 반응이라고 해석할 수 있다. 적합도가 1.6 이상이면 원인을 확인하고 반드시 수정해야 한다.
부적절한 문항을 확인하고 문항을 수정 보완하면 검사의 신뢰도를 높일 수 있다[6]. 본 연구에서 문항 적합도가 1.3 이상을 갖는 문항은 9번과 23번이었고, 이때 점양분상관계수에 의한 변별도는 -0.41과 0.07이었다. 따라서 문항 적합도와 문항 변별도가 일관된 결과를 보여주었다. 또한, 수험자 적합도는 어떤 검사의 모든 문항을 단순하게 답하거나 무작위로 답하는 수험자를 확인할 수 있고 부적합한 반응을 유발한 수험자들을 제거하면 검사의 정확도를 개선할 수 있다고 한다[13]. 본 연구에서 학생 32번은 outfit 적합도가 64.97이었고 잘못된 표기 방법에 의한 판독기 오류 때문인 것을 확인할 수 있었다.
추정된 수험자 능력과 문항 곤란도로 Fig. 3과 같이 수험자-문항 지도를 만들 수 있다. 그림의 수직축은 logit 척도이며 수험자와 문항이 어떻게 상호작용하는지 알려준다. 본 예에서 수험자의 능력에 비해 문항이 상대적으로 쉽다는 것을 Fig. 3에서 보여준다. 이러한 상호관계는 검사의 구성 타당도(construct validity)를 제공해 준다[20]. 검사를 제작할 때 필요에 따라서 문항의 곤란도를 상승하거나 하강하는 기준을 제공할 수 있다. 평균으로부터 표준편차의 2배의 값보다 큰 문항은 수험자에게 너무 어렵기 때문에 문항을 교정할 필요가 있다. Equation 2를 이용하여 수험자 능력 logit이 1.5인 학생이 곤란도가 0.3인 문항을 올바르게 답할 확률이 0.77이라는 것을 알 수 있다. 본 예에서 라쉬모형의 변별도는 1이고 곤란도가 0이기 때문에 Equation 2에 적용하여 능력 logit 척도를 0~100%의 척도로 전환할 수 있다(Fig. 2).
본 연구에서 고전검사이론에 의한 변별도 지수는 점양분상관계수, 교정된 문항총점상관계수 및 문항총점상관계수 순으로 우수하였고 라쉬모형에 의한 문항적합도와 일치하는 결과를 보였다. 따라서, 라쉬모형은 문항 곤란도와 수험자 능력을 추정할 수 있을 뿐만 아니고 문항에 대한 수험자의 반응을 평가할 수 있는 측정방법이다.
AcknowledgmentsThe authors would like to express their appreciation to the teaching assistant, Jiyun Kang for item analysis of course examinations.
Funding: This work was supported by the Research Fund from Jeju National University Hospital. (CNUH-2010-02).
Fig. 2.Scatter Plot the Raw Score vs. Examinee's Ability with Standard ErrorThe horizontal line is in logit and the vertical line is in percent.
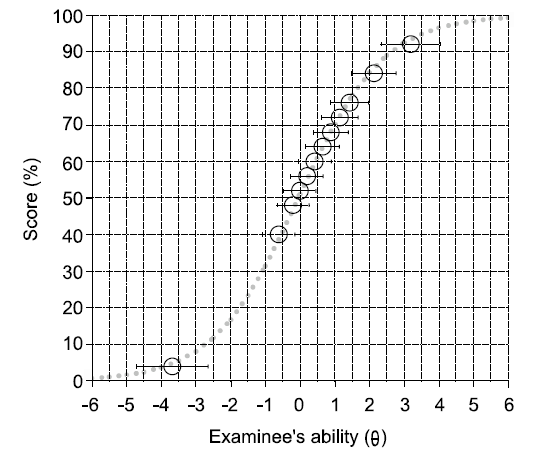
Fig. 3.Map of Item Difficulty and Examinee's Ability on Rasch Transformed Logit ScaleRight and side shows item difficulties and left had side shows the distribution of the examinee's abilities
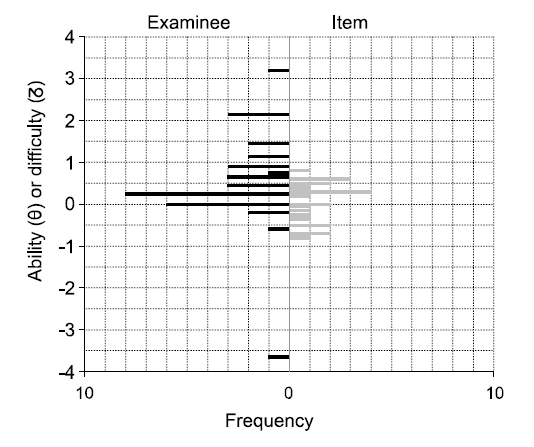
Table 1.Regression Equation between Point.Biserial Correlation (Cpbs) and Other Discrimination Indices Table 2.Examinee Characteristics of the Rasch Model and Fit Statistics
Table 3.Individual Item Difficulty and Discrimination Based on Point.Biserial Correlation (Cpbs), Item Characteristics of the Rasch Model and Fit Statistics
REFERENCES1. Fajardo LL, Chan KM. Evaluation of medical students in radiology. Written testing using uncued multiple-choice questions. Invest Radiol 1993;28:964-968.
3. Campo-Arias A, Oviedo HC, Cogollo Z. Internal consistency of a five-item form of the Francis Scale of Attitude Toward Christianity among adolescent students. J Soc Psychol 2009;149:258-262.
4. Smith RM, Suh KK. Rasch fit statistics as a test of the invariance of item parameter estimates. J Appl Meas 2003;4:153-163.
5. Karabatsos G. A critique of Rasch residual fit statistics. J Appl Meas 2000;1:152-176.
8. Willse JT. Mixture Rasch models with joint maximum likelihood estimation. Educ Psychol Meas 2011;71:5-19.
9. Baker FB. The basics of item response theory. 2nd ed. College Park, USA: ERIC Clearinghouse on Assessment and Evaluation; 2001:83-149.
10. Dinero TE, Haertel E. Applicability of the Rasch model with varying item discriminations. Appl Psychol Meas 1977;1:581-592.
11. Ji EL, Chae SH. Theory and practice of Rasch model. 2nd ed. Seoul, Korea: Kyoyukkwahaksa; 2000.
12. Brentari E, Golia S. Unidimensionality in the Rasch model: how to detect and interpret. Statistica 2007;67:253-261.
13. Linacre JM. Rasch model estimation: further topics. J Appl Meas 2004;5:95-110.
14. Ebel RL. Measuring educational achievement. 2nd ed. Englewood Cliffs, USA: Prentice-Hall; 1972.
15. Clauser BE, Ross LP, Nungester RJ, Clyman SG. An evaluation of the Rasch model for equating multiple forms of a performance assessment of physicians' patient-management skills. Acad Med 1997;72(10 Suppl 1):S76-S78.
16. Linacre JM. Understanding Rasch measurement: estimation methods for Rasch measures. J Outcome Meas 1999;3:382-405.
17. Hessen DJ. A new class of parametric IRT models for dichotomous item scores. J Appl Meas 2004;5:385-397.
18. Sijtsma K, Junker BW. Item response theory: past performance, present developments, and future expectations. Behaviormetrika 2006;33:75-102.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||